Knowledge Graphs: Modeling your understanding of an idea

In this post, I’ll give an overview of

• an example of a knowledge graph (using a college degree as a metaphor),
• why there’s no such thing as tacit knowledge, and
• how you can use knowledge graphs to model your understanding of an idea.

College Degree Plans#

Let's say you're in college, and you're trying to complete an engineering degree. To complete the degree, you have to take a set of courses.

However, you can't just take them in any order you want. Some of them have prerequisites.

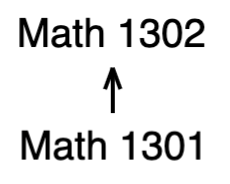
In fact, some of them have a chain of prerequisites!

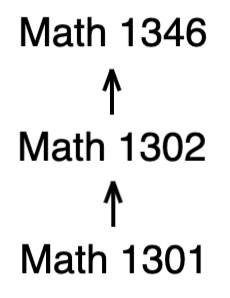
You can also have multiple prerequisites for each class.

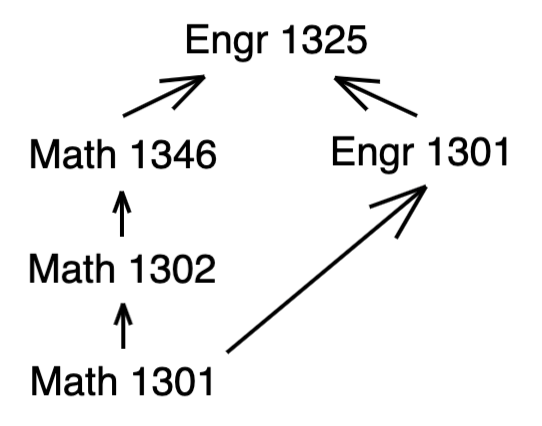
This means determining an optimal order for your degree plan can get pretty complicated. Thus, a typical strategy is to identify the classes at the bottom of each chain and take them first.

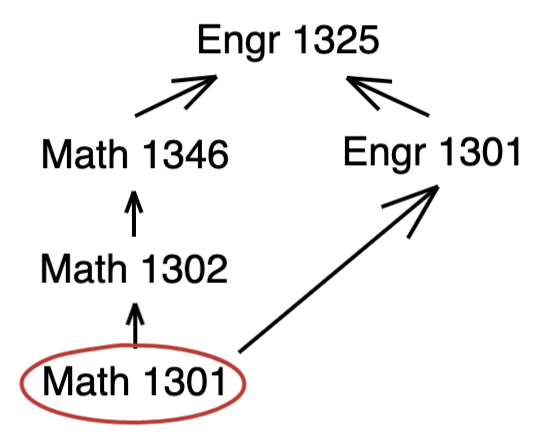
Using the above example, we can model any college degree:

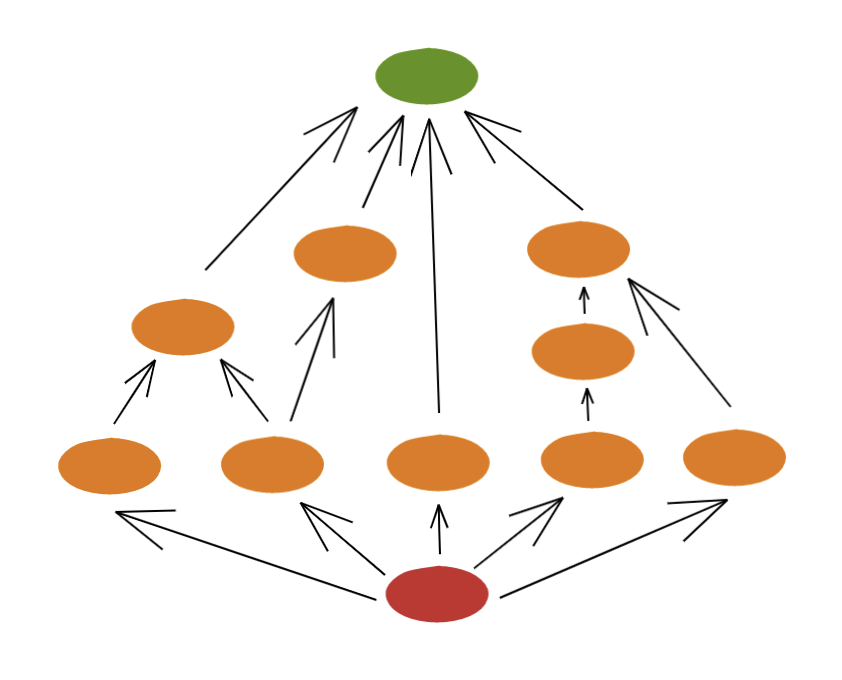
• Green is the very top: completion of the degree
• Orange is a particular class
• Red is the very beginning: Not having taken any classes.

This structure is an example of a (topologically sorted) graph (i.e. a directed graph with dependencies).

Specific Ideas#

A graph can also be helpful in understanding things on a smaller scale - including individual ideas. A topologically sorted graph of ideas is an example of a knowledge graph (for which, I don't believe there is a rigorous definition). Let's take this code for example:

let total = 0;
for (let i = 0; i < 5; i++) {
    total = total + i;
}
console.log(total);

If you're familiar with JavaScript, you know what's going on here. It’s computing 0 + 1 + 2 + 3 + 4 and then printing it.

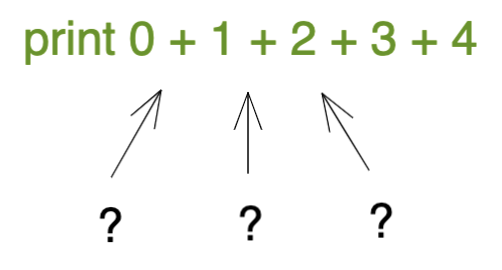
But, let's say you're not familiar. If I gave you the above high level overview of what that code does (i.e. computing the sum), it wouldn’t mean that you would then understand the details and concepts involved. Much like our college degree example earlier, there are a lot of prerequisite ideas that this “sum” code builds upon.

A similar knowledge graph would have the general idea at the top (in green), and all the prerequisite ideas below it:

Perhaps, after reading the code carefully, you've picked up on some of the lower-level concepts and increased the depth of your knowledge graph:

However, if I asked you to explain the code from scratch in laborious detail (without Googling), you would struggle (assuming you had no familiarity). Your knowledge graph isn't deep enough, yet, for that kind of fluency.

Tacit Knowledge#

It’s no surprise that people have trouble explaining concepts they’re not familiar with, but a lot of people would argue that some knowledge, dubbed tacit knowledge, is intrinsically hard to communicate or explain.

I propose that there is actually no such thing as tacit knowledge. Just because we can’t explain it well doesn’t mean it’s innately hard to explain. What is tacit for one person might be very tangible for others.

In other words, it’s not the idea itself that is tacit. It’s us. More specifically, it’s the depth of our knowledge graph for the idea. If you can’t explain it simply, you don’t understand it well enough.

You might counter by saying that some knowledge is tacit. Let’s examine a common example of tacit knowledge: how to ride a bike.

It’s true that explaining how to ride a bike to someone who doesn’t know how will, alone, not succeed. However, I would argue that it’s because both the student and teacher don’t understand riding a bike well enough.

If you understand riding a bike well enough, there are plenty of ways to describe it exactly. One such explanation could look like this:

• Raise your leg in the air
• Put your foot on the opposite side of the bike such that you’re facing forward and hovering over the seat
• Sit on the bike saddle
• Put your hands on the front handles
• Put both feet on the pedals
• Now, instantaneously, you will start falling.
• From second 0 to second 1:
  • contract your quadricep at 25% capacity
  • contract your calf at 37% capacity
  • …etc, for all muscles involved in biking
• From second 1 to second 2:
  • contract your quadricep at 35% capacity
  • contract your calf at 28% capacity
  • …etc, for all muscles involved in biking

And so on. The explanation is specific, verbose, and complete (i.e. anything but tacit).

In fact, once we remove the channel (i.e. verbal instruction) as a factor, we uncover the real culprits that block understanding: a working memory bottleneck and lack of appropriate long term memories. If at least one of these limits didn’t exist, the knowledge could be communicated effectively.

For example, if the student had unlimited working memory, then, as long as the instructions were specific enough, delivering instructions to the student would be analogous to programming a computer.

Alternatively, if the student had an appropriate set of long term memories, such as riding a motorcycle, then the teacher could just say something like, “It’s like riding a motorcycle, except instead of an engine, you peddle.”

Modeling an Idea#

Let's go back to the code example:

let total = 0;
for (let i = 0; i < 5; i++) {
    total = total + i;
}
console.log(total);

How would we enumerate the full knowledge graph for this code? Let's start with the fundamentals at the bottom.

...Well, hm. That's unexpectedly hard. We can go arbitrarily deep.

We can sink down to the hardware level. We can go deeper and talk about physics. We can get really meta. It's possible that this knowledge graph is infinitely complex.

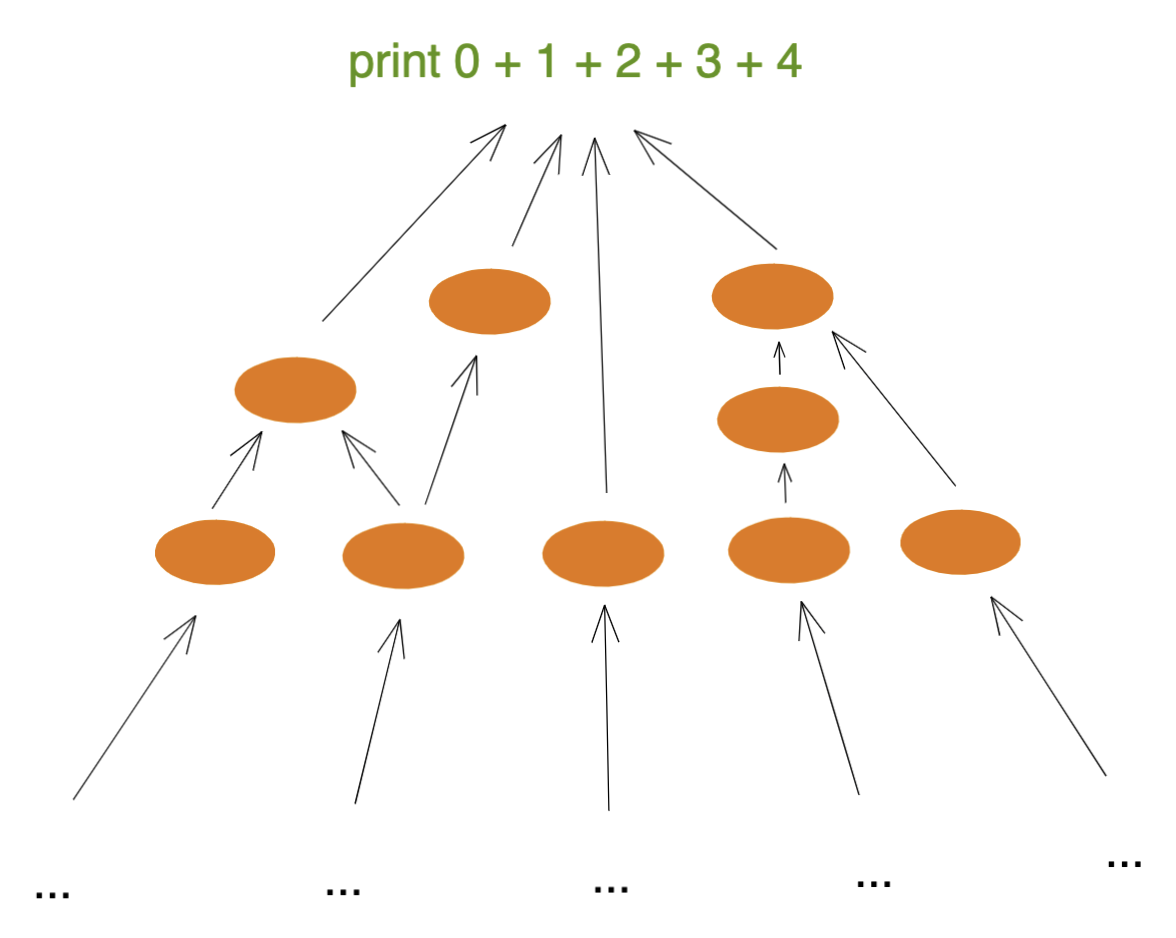
This is a somewhat profound idea: it implies that, for any given idea, there is no such thing as "the fundamentals" - you can always deepen your understanding.

Perhaps what we know as "the fundamentals" from a given field are better described as the set of ideas that act as the greatest common denominators for the field in general. Another way of looking at it: the fundamentals are the set of ideas that act as minimally leaky abstractions for ideas further down the graph. These are ideas that you can trust to act as a foundation for more complex ideas.

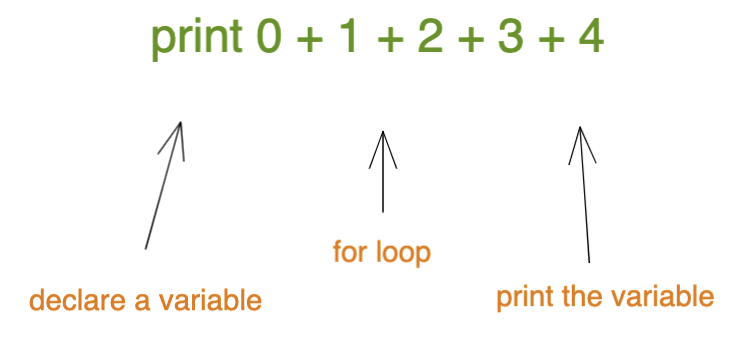
Let us, instead, start at the top and traverse down until it stops seeming like a good idea.

The code does three things:

• declares a variable: let total = 0
• iteratively adds an increasing number to it: for (...)
• prints the variable out: console.log(total)

So, at this point, our knowledge graph looks like this:

Now, for each of our 3 nodes, let's talk about what concepts we need to understand them:

• declare a variable
  • what let means
  • what a variable (total) is
  • what does variable assignment (total = 0;) mean
• iteratively add an increasing number to it
  • what does that syntax (( ... ; ... ; ...)) mean?
  • what i++ means
  • what let means
  • what the brackets ({}) mean
  • what variable assignment means (total = total + i)
• print the variable out
  • what does console mean?
  • what does log mean?

Here's what our updated knowledge graph might look like:

Wow, that's already getting really crazy. But, it's a good opportunity to point out how hard teaching actually is.

Because each student has a different proficiency, each of their knowledge graphs has a different depth. Worse, still, each branch of each graph has its own depth!

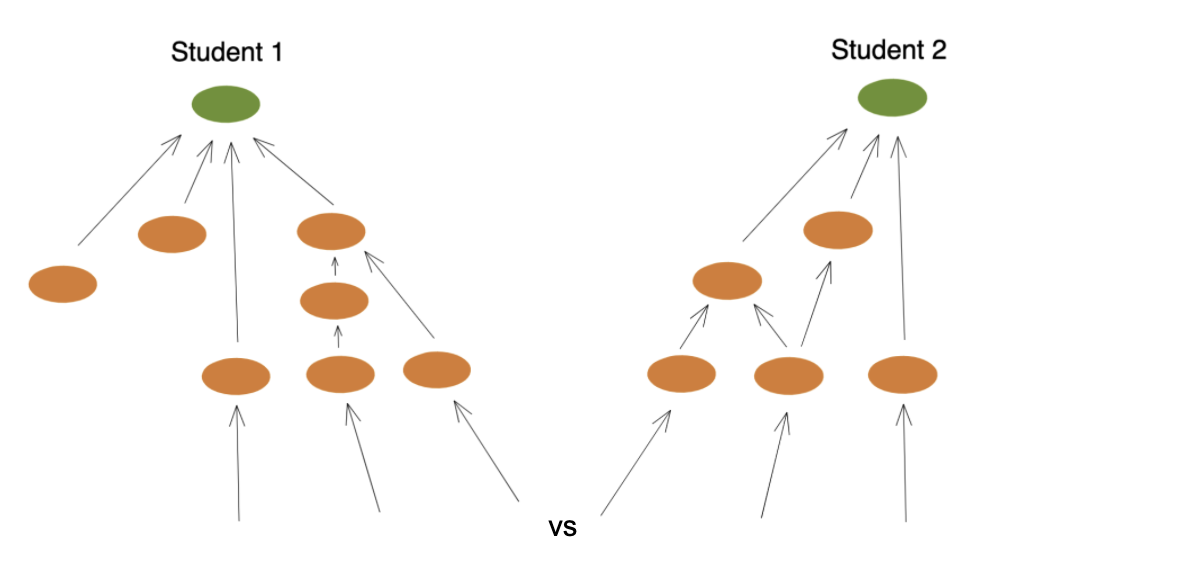
This means it's entirely possible for students to oscillate back and forth between bored and confused, depending on the lesson.

No wonder professors just give up and lecture. If they don't get it, they'll come to office hours.

How Knowledge Graphs Can Help You Learn#

Modeling information this way can be helpful in the following ways:

• Measuring, with more precision and granularity, how well you understand an idea (i.e. the deeper your knowledge graph the more you understand it)
• Organizing what you know (you get a nice visualization for free!)
• Identifying the parts you are less knowledgeable on (whenever you get to the bottom and it feels shaky, that’s an area you should work on)
• Understanding complex ideas (you can look at the big picture or the details!)

In fact, creating a knowledge graph for a particular idea is similar in spirit to something you’ve probably heard of:

The Feynman Technique

Structurally, the Feynman Technique is doing a breadth-first traversal of a knowledge graph, starting at the top!

Hence, an algorithm for helping yourself learn an idea might be:

• Start at the top of a sheet of paper, and write down the idea in as much detail as you can.
• Then, reread what you wrote, and for any word, phrase, formula, etc that you aren’t 100% confident you understand, circle it.
• Below what you wrote, for every circled item, write down everything you know about the item that relates to the idea, looking things up as needed.
• Think about the relationships between everything you’re writing. If they’re not obvious, look that up as well.
• Again, reread everything you wrote, and circle things you don’t understand.
• Rinse and repeat until you understand everything you’ve written down!

Happy learning!

Thank you to the Compound Writing members who reviewed this post: Tyler Wince, Stew Fortier, and Patrick Rivera.